Author: National Renewable Energy Laboratory[1]
The full converter wind turbine (FCWT) employs a permanent magnet alternator (PMA). This technology has a number of significant advantages[2]. It effectively decouples the generator from the grid, improving fault response. It allows the turbine to operate over a wide speed range, leading to improved power extraction from the wind. The converter interfacing the turbine to the grid has to handle the entire output of the generator (unlike in a DFIG turbine where the converter handles only 30% to 40% of the generator output) and hence is more costly and lossy, but also provides more headroom to supply reactive power to the grid. The permanent magnet alternator (PMA) itself has no rotor windings, reducing excitation losses and reducing the size of the generating unit with respect to competing technologies. Absence of rotor slip rings reduces maintenance requirements. This combination of factors is driving the increasing penetration of FCWTs, especially for offshore wind power plants.
The popularity of FCWTs has led to a search for reliable models to evaluate the impacts of integrating these FCWTs into the existing grid. The model presented in this article is a generic, manufacturer-independent model for a PMA-based FCWT, with no restrictions on its use. The converter topology of the model described below is a popular one; the PMA is interfaced to the grid through an AC-DC-AC conversion system. The AC-DC converter is comprised of a diode-bridge rectifier and a buck-boost converter which controls the DC link voltage. The DC-AC conversion is accomplished using a current-controlled inverter which controls the real and reactive output power. Although the focus in this article is on the specific topology mentioned, various converter topologies can be modeled with simple modifications using the same framework. In the past FCWT models with an entirely different topology using this framework have been developed[3]. The mechanical and aerodynamic components of the model presented here are identical to those presented in[3].
The complete model has been implemented in PSCAD/EMTDC for the purposes of this article. However, the model is straightforward to implement using other popular simulation packages such as MATLAB/Simulink. The model is based on parameters from an Enercon E82 2-MW turbine.
Contents
- 1 Model Development
- 1.1 Aerodynamic Block
- 1.2 Mechanical Drive-Train
- 1.3 Reference Power Calculation from Wind Speed
- 1.4 Pitch Control Block
- 1.5 Permanent Magnet Alternator
- 1.6 Rectifier and Buck/Boost Converter for DC-Link Voltage Control
- 1.7 Inverter
- 1.8 Unit Transformer and Grid Representation
- 1.9 Complete Model Implemented in PSCAD/EMTDC
- 2 Model Testing
- 3 Dynamic Response
- 4 References
Model Development
| Turbine Properties | |
|---|---|
| Turbine make | Enercon E82 2MW |
| Regulation method | Pitch control (enabled) |
| Rotor diameter | 82 m |
| Hub height | 78 m |
| Number of blades | 3 |
| Cut-in wind speed | 4 m/s |
| Cut-out wind speed | 28 m/s |
| Rated wind speed | 15 m/s (14 m/s used) |
| Rotor speed | 6/18 rpm |
From a modeling standpoint, a full converter PMA wind turbine consists of the following mechanical and electrical subsystems:
- Aerodynamic model for rotor;
- Mechanical two-mass model for drivetrain;
- Reference power calculation block;
- Pitch controller;
- Permanent magnet alternator (PMA) model;
- Rectifier and buck/boost converter models (for DC-link voltage control);
- Inverter model (current-controlled VSI);
- Unit transformer and grid representation.
The interaction between each of the components listed above determines the wind turbine model’s steady-state and dynamic response. Each of these subsystems presents a unique modeling challenge. Modeling of the aerodynamics and mechanical drive-train is based on the differential and algebraic equations that describe their operation. Reference power is currently calculated based on wind speed, though in the future it will be calculated based on rotor speed. The pitch controller currently utilizes both power and rotor speed inputs, though it too will be modified in the future to only use rotor speed as input. A general PMA model is available in PSCAD/EMTDC which can be modified to serve the purposes of this model. The rectifier, buck/boost converter and inverter are modeled explicitly using diode and IGBT models supplied with PSCAD/EMTDC. Details for each of the subsystems are presented in the following subsections.
Aerodynamic Block
The aerodynamic block consists of three subsystems: tip-speed ratio calculation, rotor power coefficient (CP) calculation, and aerodynamic torque calculation. Wind speed and pitch angle are user-defined inputs. Since the model is intended to study the dynamic response of wind turbines to grid events, the assumption is usually made that the wind speed stays constant during the grid event. However, this model allows the wind speed input signal to be set to any value at the start of the simulation run-time and also to be modified during the run. It is also possible to use a time-series of actual wind speed data.
Tip-Speed Ratio Calculations
The tip-speed ratio or TSR, denoted by λ, is the ratio of the blade-tip linear speed to the wind speed[4]. The TSR determines the fraction of available power extracted from the wind by the wind turbine rotor. The TSR can be calculated as follows
\(\lambda=\frac{\omega_{rotor} · R_{rotor}}{V_{wind}}\)where,
ωrotor = rotor angular speed [rad/s]
Rrotor = rotor radius [m]
Vwind = wind speed [m/s]
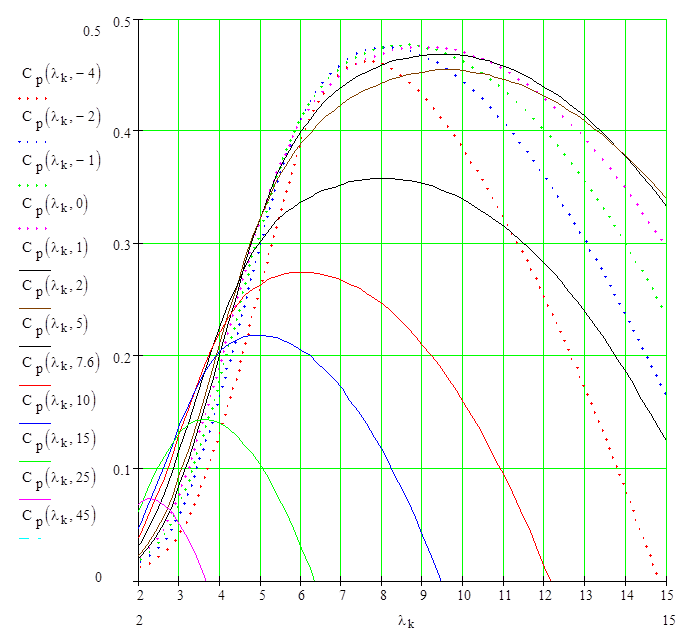
Rotor Power Coefficient (Cp) Calculation
The TSR, together with the user-defined blade pitch angle β, are used to calculate the rotor power coefficient, denoted by CP. The rotor power coefficient is a measure of the rotor efficiency and is defined as
\(\mathrm{C}_P=\frac{Extracted\ Power}{Power\ in\ Wind}=\frac{P_{rotor}}{P_{wind}}\)There is a constant value of λ which, if maintained for all wind speeds, will result in an optimal CP curve and optimal power extraction from the wind. Variable-speed wind turbines are equipped with a pitch-change mechanism to adjust the blade pitch angle and obtain a better power coefficient profile. In the model, a set of generic CP curves are used to calculate the value of CP[5].
Aerodynamic Torque Calculation
The kinetic energy E (in J) of an air mass m (in kg) moving at a speed Vwind (in m/s) is given by[4]
\(E=\frac{1}{2}mV_{wind}^2\)
If the air density is ρ (kg/m3), mass flow through an area A is given by
\(\dot{m}=ρAV_{wind}\)
Thus, an equation for the power (in W) through a cross-sectional area A normal to the wind is
\(P_{wind}=\frac{1}{2}ρAV_{wind}^3\)
In the case of a wind turbine, area A is the area swept by the rotor blades. Only a part of this power may be captured due to the non-ideal nature of the rotor, hence the need for the coefficient CP.
\(P_{rotor}=\frac{1}{2}ρ\cdot\mathrm{C}_p\cdotπ\cdot\mathrm{R}_{rotor}^2\cdot\mathrm{V}_{wind}^3\)
The aerodynamic torque developed (in Nm) can then be calculated
\(\Gamma_{rotor}=\frac{P_{rotor}}{ω_{rotor}}=\frac{\frac{1}{2}\cdotρ\cdot\mathrm{C}_p\cdotπ\cdot\mathrm{R}_{rotor}^2\cdot\mathrm{V}_{wind}^3}{ω_{rotor}}\)
Mechanical Drive-Train
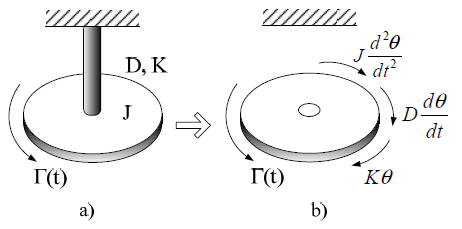
The mechanical block consists of the rotor shaft, generator shaft, and a gearbox. The shafts and the gearbox are modeled using a two-mass inertia representation. For a rotational system[6], consisting of a disk with a moment of inertia J mounted on a shaft fixed at one end, let us assume that the viscous friction coefficient (damping) is D and that the shaft torsional spring constant (stiffness) is K. The torque acting on the disk can be calculated from the free-body diagram of the disk, as follows
\(\Gamma(t)=J\frac{d^2\theta(t)}{dt^2}+D\frac{d\theta(t)}{dt}+K\theta(t)\)
A more complex rotational system consists of two such systems. The two systems are coupled through a gear train, and Γ is the external torque applied to the disk of System 1. Γ1, Γ2 are transmitted torques. N1, N2 are the numbers of teeth of Gear 1 and Gear 2. J1, J2, D1, D2, K1, K2 are the moments of inertia, damping, and stiffness of System 1 and System 2, respectively. The system is still time-dependent, but the notation t is dropped for the sake of clarity.
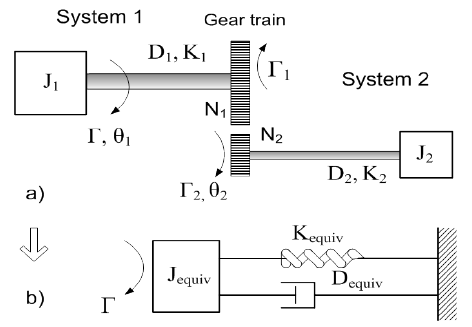
The torque equation at J1 can then be calculated as
\(\Gamma_1=J_1\frac{d^2\theta_1}{dt^2}+D_1\frac{d\theta_1}{dt}+K_1\theta_1\)
The torque equation at J2 can then be calculated as:
\(\Gamma_2=J_2\frac{d^2\theta_2}{dt^2}+D_2\frac{d\theta_2}{dt}+K_2\theta_2\)
Since Γ1 = (N1/N2)Γ2 and Θ2 = (N1/N2)Θ1, the quantities on Gear 2 side can be referred to the Gear 1 side[6].
\(\Gamma_1=\left (\frac{N_1}{N_2} \right)\left (J_2\frac{d^2\theta_2}{dt^2}+D_2\frac{d\theta_2}{dt}+K_2\theta_2 \right)\)
\(\Gamma_1=\left (\frac{N_1}{N_2} \right)\left [J_2\left (\frac{N_1}{N_2} \right)\frac{d^2\theta_1}{dt^2}+D_2\left (\frac{N_1}{N_2} \right)\frac{d\theta_1}{dt}+K_2\left (\frac{N_1}{N_2} \right)\theta_1 \right]\)
\(\Gamma_1=J_{refl}\frac{d^2\theta_1}{dt^2}+D_{refl}\frac{d\theta_1}{dt}+K_{refl}\theta_1\)
where Jrefl, Drefl, and Krefl are the quantities reflected on the Gear 1 side. Substituting the above equations and rearranging them, we obtain the equation for the applied torque. The gear train is eliminated in the equivalent system.
\(\Gamma=J_{equiv}\frac{d^2\theta_1}{dt^2}+D_{equiv}\frac{d\theta_1}{dt}+K_{equiv}\theta_1\)
where,
\(J_{equiv}=J_1+J_2\left (\frac{N_1}{N_2} \right)^2=J_1+J_{refl}\)
\(D_{equiv}=D_1+D_2\left (\frac{N_1}{N_2} \right)^2=D_1+D_{refl}\)
\(K_{equiv}=K_1+K_2\left (\frac{N_1}{N_2} \right)^2=K_1+K_{refl}\)
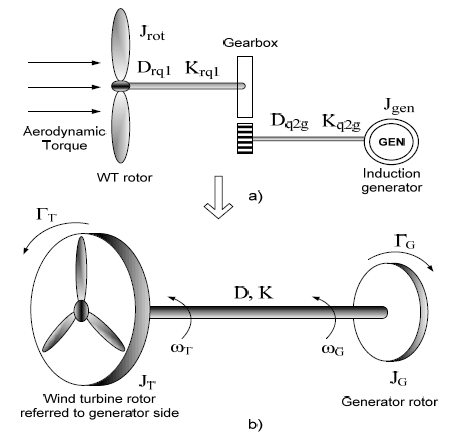
The wind turbine drive-train can therefore be modeled as a two-mass system coupled through a gear train. The quantities on the wind turbine rotor side of the gearbox can be reflected to the generator side. This eliminates the gear ratio and results in a two-mass representation of the wind turbine. Neglecting the effects of the gearbox moment of inertia, damping, and stiffness is justifiable since the moment of inertia of the wind turbine rotor is comparatively very high.
Torque equations representing the mechanical behavior of the wind turbine are derived, based on the two-mass model. The aerodynamic torque from the wind turbine rotor and the electromechanical torque from the direct-connect induction generator act in opposition to each other. Torque equations with all quantities referred to the generator side are
\(J_T\ddot {\theta_T}+D(ω_T-ω_G)+K(\theta_T-\theta_G)=\Gamma_T\)
\(J_G\ddot {\theta_G}+D(ω_G-ω_T)+K(\theta_G-\theta_T)=-\Gamma_G\)
where,
JT, JG = moments of inertia of the wind turbine rotor and the generator kgmm
ΓT, ΓG = wind turbine aerodynamic and generator electromagnetic torque Nm
ωT, ωG = wind turbine rotor and the generator speed rad/s
ΘT, ΘG = angular position of the rotor and the generator rad
D, K = equivalent damping and stiffness Nms/rad, Nm/rad
Speeds and torques of the turbine rotor and the generator can be determined for each simulation time step by solving the above equations using a state-space approach. The state-space equations are:
\(\frac{d}{dt}(\theta_G-\theta_T)=(ω_T-ω_G)\):
\(\dot {\omega_T}=\left (\frac{1}{J_T} \right)\left [\Gamma_T-D(\omega_T-\omega_G)-K(\theta_T-\theta_G) \right]\):
\(\dot {\omega_G}=\left (\frac{1}{J_G} \right)\left [D(\omega_T-\omega_G)+K(\theta_T-\theta_G)-\Gamma_G \right]\)
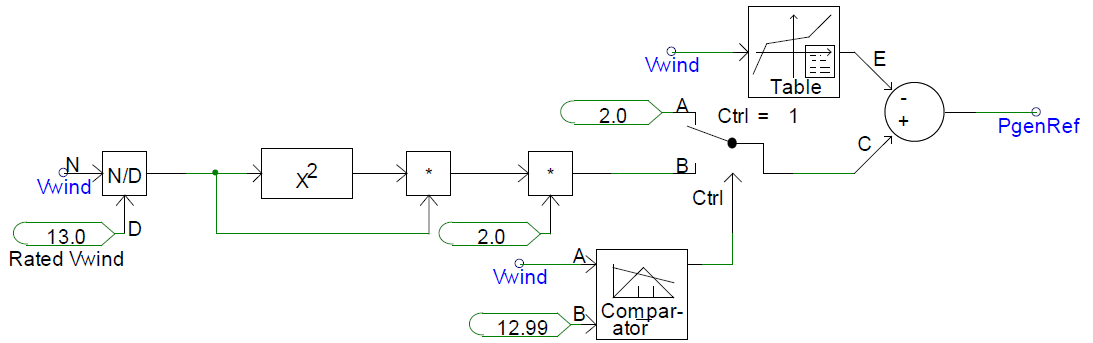
Reference Power Calculation from Wind Speed
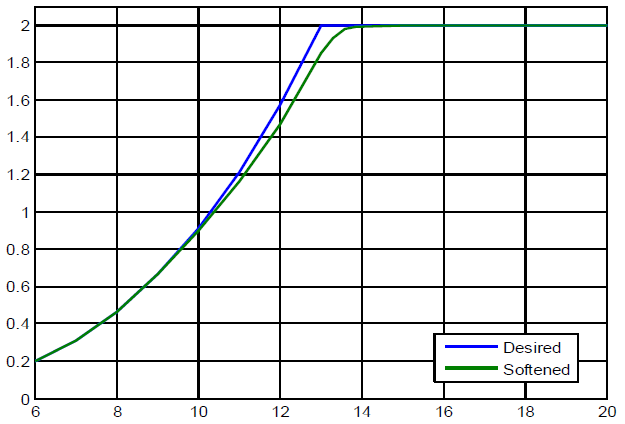
The reference power calculation is based on user-defined wind speed. Wind speed is per unitized based on rated wind speed, cubed and multiplied by rated power (2 MW) to get output power. If user-defined wind speed exceeds rated wind speed (13 m/s), output power is fixed to 2 MW. A table-based characteristic is used to remove sharp changes from the power output curve. This “softening” of the power curve is discussed in the model testing section.
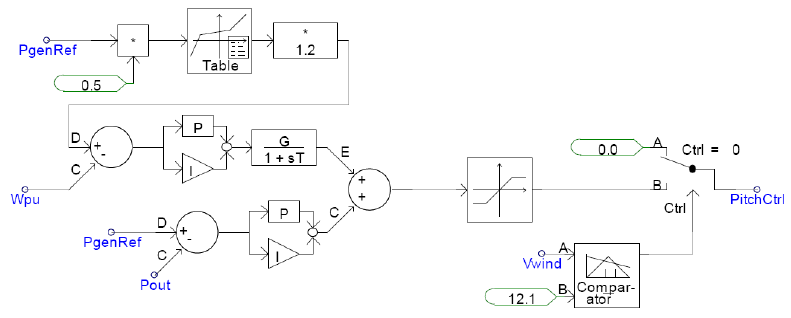
Pitch Control Block
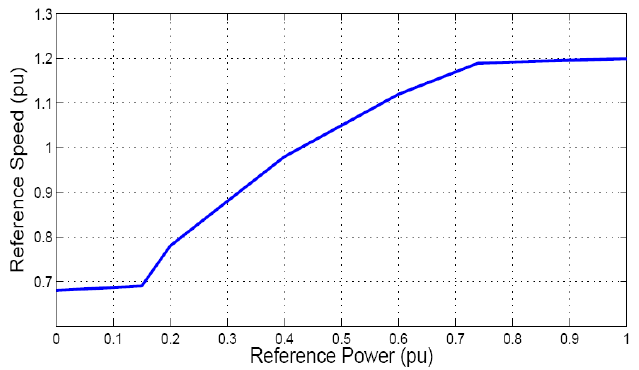
The pitch control block changes blade pitch angle at higher than rated wind speeds to spill excess power. Thus power output is maintained at rated value even though wind speed exceeds rated wind speed. In this particular implementation, reference power is per unitized and converted to reference speed based on look-up table. A multiplier after the look-up table is included to maintain stability. The reference speed and actual speed are compared, and the error drives the upper PI controller. Reference power and actual power are also compared and the error drives the lower PI controller. PI controller outputs are summed and hard-limited to generate the pitch angle signal. The pitch angle signal is active only when wind speed is close to rated, and otherwise is fixed at zero.
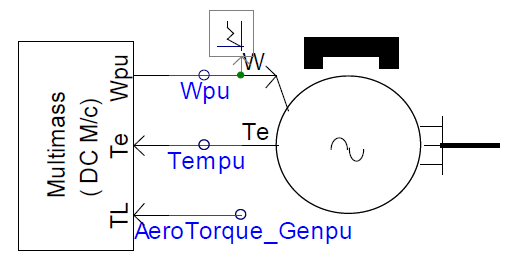
Permanent Magnet Alternator
The permanent magnet alternator is modeled using a built-in PSCAD/EMTDC PMA block.
 |
|
||||||||||||||||||||||||||||
Rectifier and Buck/Boost Converter for DC-Link Voltage Control
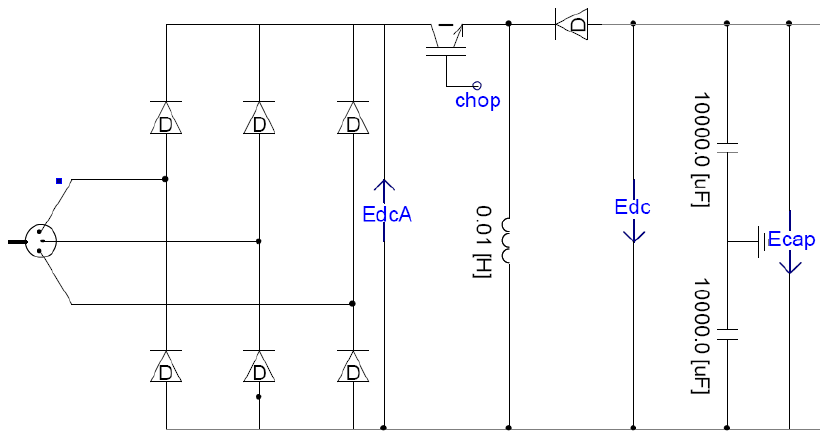
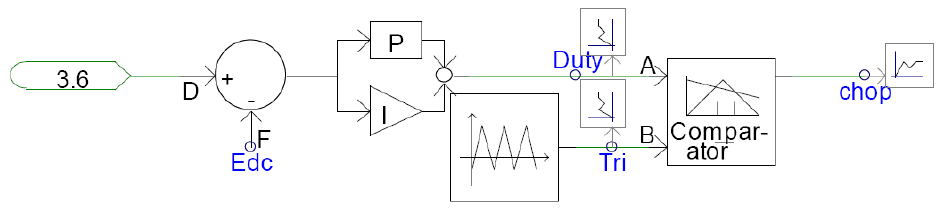
The rectifier and buck/boost converter models are responsible for converting the AC output of the PMSG to a fixed DC voltage. An example of the use of buck/boost converters for DC link control for PMA wind turbines is provided in literature[7]. A 3-phase diode bridge converts PMA output to a variable DC voltage. The buck-boost converter maintains the DC link at a constant 3.6 kV. The DC link capacitor is modeled as two identical capacitors with ground in between them due to PSCAD/EMTDC ground reference issues. This controller is based on PI control; any error between the desired voltage set-point (3.6 kV here) and the actual voltage drives the PI controller and generates a duty signal output. The duty signal is compared to a triangle wave to generate firing signals for the IGBT in the buck/boost converter.
Inverter
.png)
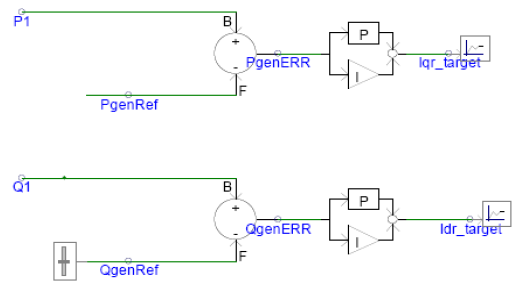
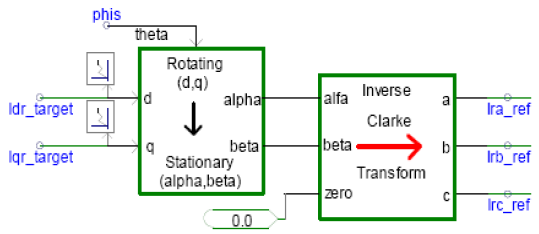
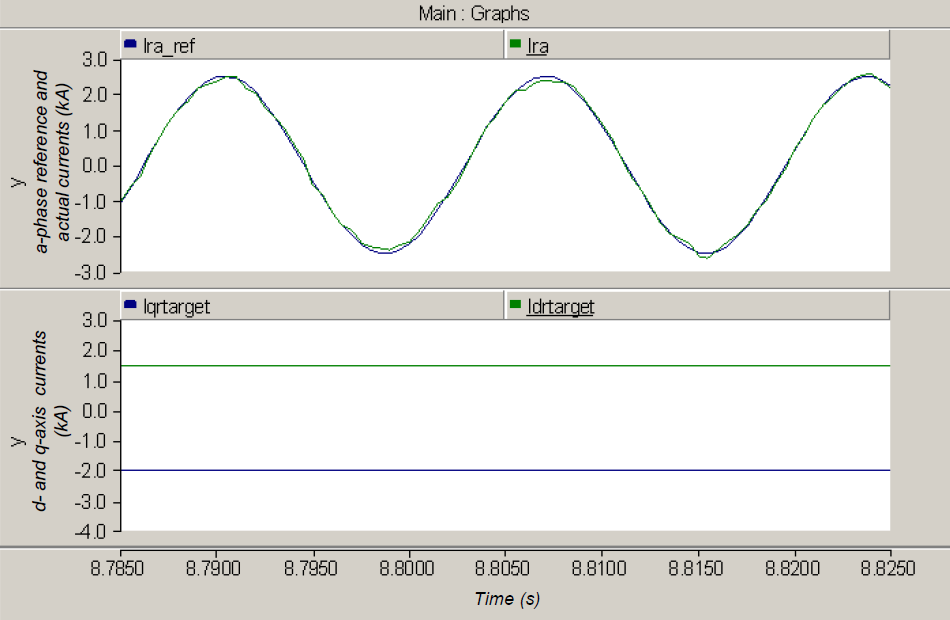
The inverter implemented here is a current controlled voltage-source inverter. It is capable of decoupling real and reactive power control, since the controller design for this inverter is based on flux-vector theory. Real and reactive power reference signals are compared with actual values and the error is used to drive two independent PI controllers. The real power error drives the Iq signal, while reactive power error drives the Id signal. These dq0 domain values are converted to reference Iabc values (note that the angle signal phis is calculated from the voltage phasor). The reference Iabc currents are compared with actual currents and a hysteresis controller switches the inverter IGBTs such that actual current follows the reference current. When the reference currents are achieved, reference real and reactive power is also achieved. The actual current can be seen to be closely following the reference current.
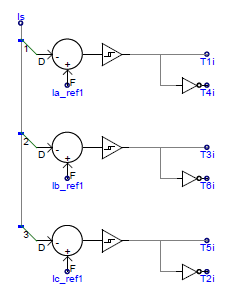 |
 |
Unit Transformer and Grid Representation
The unit transformer and grid are both modeled using in-built blocks supplied by PSCAD/EMTDC. The unit transformer is a wye-delta 2-MVA transformer with a primary voltage of 34.5 kV and a secondary voltage of 0.6 kV, and a per unit leakage reactance of 0.1 p.u. During the development and testing phase, the grid is represented by a 34.5-kV voltage source.
Complete Model Implemented in PSCAD/EMTDC
_Type4.png) |
 |
Model Testing
The model testing phase is essential to evaluate the capabilities of the model. The model testing phase has three main objectives:
- To verify that desired wind turbine power curve is achieved;
- To demonstrate independent real and reactive power control;
- To demonstrate pitch controller action.
If the model is able to meet these objectives, we can use it with confidence as a platform for modeling more advanced controls, such as providing inertia and frequency response.
Power Curve
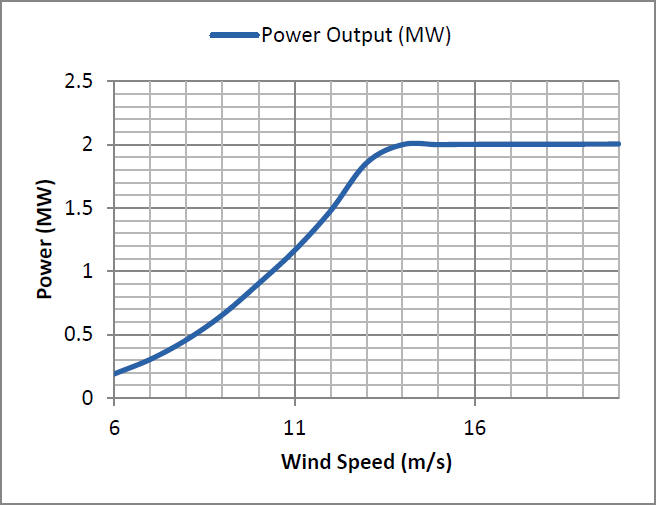
The desired power curve is a cubic function of per unit wind speed (up to rated wind speed). Rated power is achieved at rated wind speed. Beyond rated wind speed, the desired power is flat at rated power. Thus, the curve has sharp edge at rated wind speed. This edge needs to be smoothed out, or else the model will have stability issues around the rated wind speed. The smoothed curve is the one actually implemented in the reference power calculation block discussed earlier. Rated power is thus achieved at 14 m/s rather than 13 m/s. The obtained results show that the power output tracks the desired (softened) curve closely. The plot is obtained from a PSCAD/EMTDC simulation multi-run to ensure that the power output measured for each wind speed is the steady-state value. Thus, we can claim that that the first objective, that of achieving the desired power curve, is met.
 |
 |
|
||||||||||||||||||||||||||||||||||
Independent Real and Reactive Power Control
To test if independent real and reactive power control has been achieved, four tests were carried out: real power drop, reactive power drop, real power rise, and reactive power rise. Each of these is modeled as a step change, i.e., at a particular instant, the simulation was paused and a step change was made to either the wind speed or reactive power demand. In the first test, a real power drop was simulated. The wind speed was changed from 13 m/s to 11 m/s at t=12s. The reactive power demand was set at 0.4 MVAR. The real power output drops and settles to the new value. Reactive power drops initially, but recovers to the original value. In the second test, a reactive power drop was simulated. The wind speed remains at 13 m/s throughout the run, but reactive power demand was changed from 0.5 MVAR to 0.2 MVAR at t=12s. The reactive power dropped, as expected. The real power output shows a slight perturbation, but recovers to the original value. In the third test, a real power rise was simulated. The wind speed was changed from 11 m/s to 15 m/s at t=12s. The reactive power demand was set at 0.4 MVAR. The real power output rises and settles to the new value. Reactive power rises initially but recovers to the original value. In the fourth test, a reactive power rise was simulated. The wind speed remains at 13 m/s throughout the run, but reactive power demand was changed from 0.5 MVAR to 0.7 MVAR at t=12s. The reactive power rose, as expected. The real power output once again shows a slight perturbation but recovers to the original value.
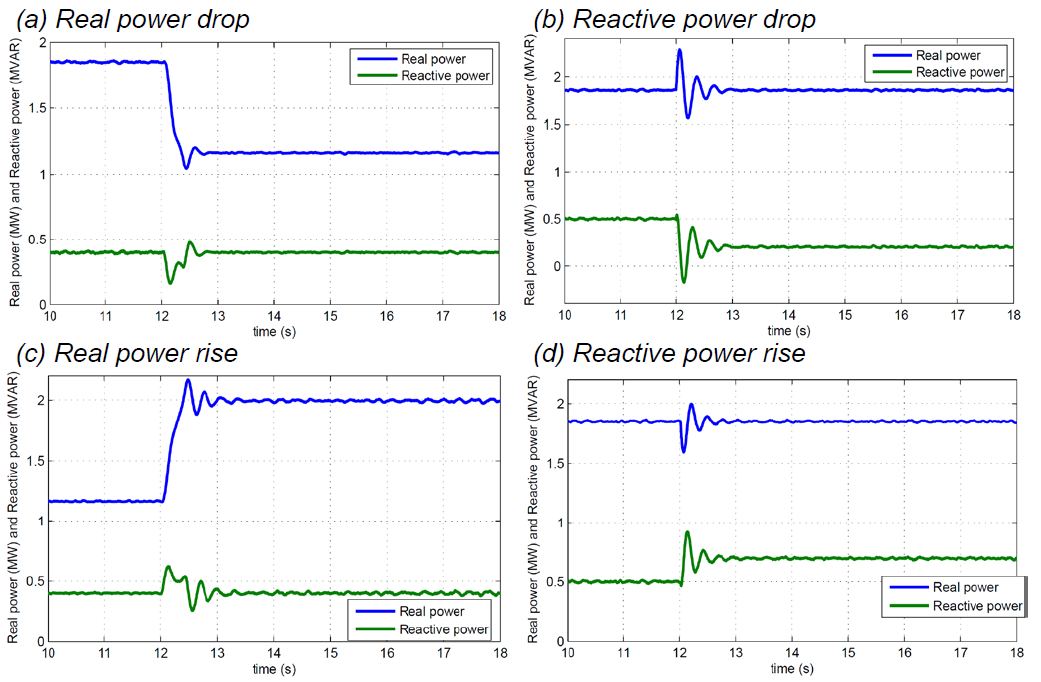 |
Consider the real power drop. In this case, when wind speed drops suddenly, the pitch controller is de-activated, and the pitch angle moves quickly to zero. This is likely the cause for the overshoot observed in the power waveform. Within the wind turbine control system, the change in wind speed changes the Pgenref value. At this instant, the error between Pgenref and the actual power output becomes large, driving a change (reduction) in the value of q-axis current Iq. The d-axis current does not change since the reactive power set-point is not changed. This change in Iq leads to a corresponding change in the three-phase currents, leading to the desired change in the real power output. The reactive power output stays constant at the set-point. It should be noted that the decoupling effect observed here for Type 4 turbines is even more pronounced than in the Type 3 turbine, especially under the transient conditions. The reason for this is that the Type 4 turbine is completely decoupled from the grid, unlike the Type 3 turbine in which flux linkages in the stator can be momentarily affected by transients on the grid side. The results here conclusively show that a change in either real power or reactive power demand does not affect the other quantity. Based on the results of the testing, we can claim that the objective of independent real and reactive power control has been achieved.
Pitch Control
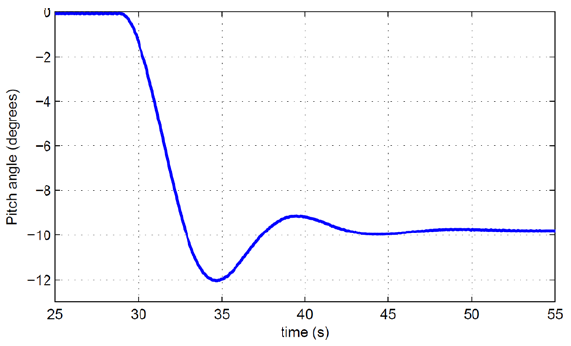
A test was devised to evaluate pitch controller action. The wind speed changed from 11 m/s to 15 m/s at t=25s. The pitch angle was initially at 0 degrees (i.e., the pitch controller was inactive). From the obtained results, it can be seen that the pitch controller becomes active when wind speed change occurs. This occurs due to new wind speed (15 m/s) being higher than rated. Eventually, the pitch angle settles close to -8 degrees, effectively spilling some excess power. It should be noted that the pitch angle values are inverted (negative rather than positive) due to the CP lookup table characteristics; -8 degrees here thus corresponds to 8 degrees in the real world. The test shows that the pitch controller does indeed work in a stable fashion.
Dynamic Response
To demonstrate the model’s ability to reproduce wind turbine dynamics, a test was created. The wind turbine was operated with a constant wind speed (15 m/s). This wind speed was higher than rated wind speed and hence, the pitch controller was active. A voltage sag on the grid was simulated, and the real and reactive power response of the wind turbine was observed. Note that this is not an implementation of low-voltage ride through (LVRT), but rather a test of dynamic response. The grid voltage drops from 1 p.u. to 0.6 p.u. at t=30s, and the sag persists for 18 cycles (0.3 seconds). The intent of the test is to show that the model does indeed respond to events occurring in the dynamic timescale and that the response of the machine to this event is realistic. The obtained results show that the model does indeed respond to the grid event as expected. The grid voltage, converter current demand, real power and reactive power, rotor speed, and pitch angle during the event are shown.
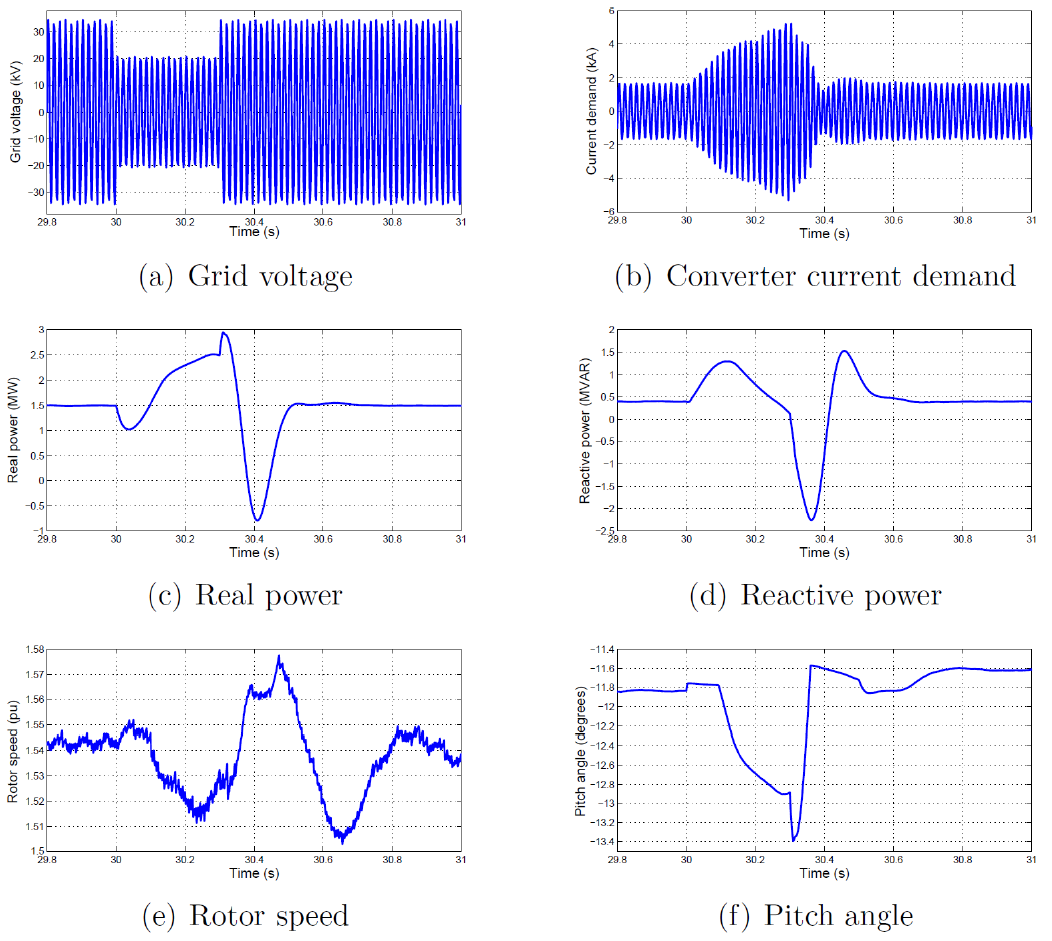 |
From the obtained results it can be seen that real and reactive power show a sharp increase when the event starts. This is due to the grid-side converter attempting to maintain real power output at 2 MW despite the voltage drop occurring. The converter greatly increases the current demand from the generator, which reflects as a jump in power. The pitch controller also seeks to maintain real power output at 2 MW, and hence, begins to move to a lower angle to counter the effects of the converter action. Based on these results, we can say that the model is behaving as expected, and realistic explanations for the response can be offered. The transients when the voltage sag occurs and when the sag ends are also visible. We can thus claim that the model described here offers good resolution and detail. This event is similar to the event used for testing purposes in literature[8], which offers a useful comparison: the voltage drop was from 1 p.u. to 0.5 p.u. and the sag persisted for 0.5 seconds. The power electronic converters are not explicitly modeled in literature[8], and the topology and controls are also different from those presented here, leading to a considerable difference in results.
References
- ↑ NREL, Dynamic Models for Wind Turbines and Wind Power Plants (NREL/SR-5500-52780), October 2011, [Online]. Available: http://www.nrel.gov/docs/fy12osti/52780.pdf. [Accessed February 2013].
- ↑ A. Perdana and O. Carlson, “Aggregated Models of a Large Wind Farm Consisting of Variable Speed Wind Turbines for Power System Stability Studies,” in Proceedings of 8th International Workshop on Large-Scale Integration of Wind Power into Power Systems as well as on Transmission Networks for Offshore Wind Farms, (Bremen, Germany), October 2009.
- ↑ 3.0 3.1 M. Singh, M. Vyas, and S. Santoso, “Using generic wind turbine models to compare inertial response of wind turbine technologies,” in IEEE Power and Energy Society General Meeting, (Minneapolis, MN), July 2010.
- ↑ 4.0 4.1 J. Manwell and J. McGowan, Wind energy explained: theory, design and application. Wiley Chichester, 2003.
- ↑ R. Delmerico, N. Miller, W. Price, and J. Sanchez-Gasca, “Dynamic Modeling of GE 1.5 and 3.6 MW Wind Turbine-Generators for Stability Simulations,” in IEEE Power Engineering Society General Meeting, (Toronto, ON).
- ↑ 6.0 6.1 B. Kuo, Automatic control systems. Prentice Hall, 1995.
- ↑ T. Tafticht, K. Agbossou, and A. Cheriti, “DC bus control of variable speed wind turbine using a buck-boost converter,” in IEEE Power Engineering Society General Meeting, (Montreal, QC), July 2006
- ↑ 8.0 8.1 J. Morren, J. Pierik, and S. de Haan, “Voltage dip ride-through control of direct-drive wind turbines,” in 39th International Universities Power Engineering Conference, vol. 3, (Bristol, UK), pp. 934 – 938, 2004.
